Understand Best Subset Selection

When building a regression model, removing irrelevant variables will make the model easier to interpret and less prone to overfit the data, therefore more generalizable.

Best subset selection is a method that aims to find the subset of independent variables (X_i) that best predict the outcome (Y) and it does so by considering all possible combinations of independent variables.

We will start by explaining how this method works and then we will discuss its advantages and limitations.

So let’s get started!

How best subset selection works

If we have k independent variables under consideration, best subset selection:

Starts by considering all possible models with 1 variable, 2 variables, …, k variables
Then chooses the best model of size 1, the best model of size 2, …, the best model of size k
Lastly, from these finalists, it chooses the best overall model

Best subset selection ends up selecting 1 model from 2^k possible models.

Here’s an example of best subset selection with 3 variables:

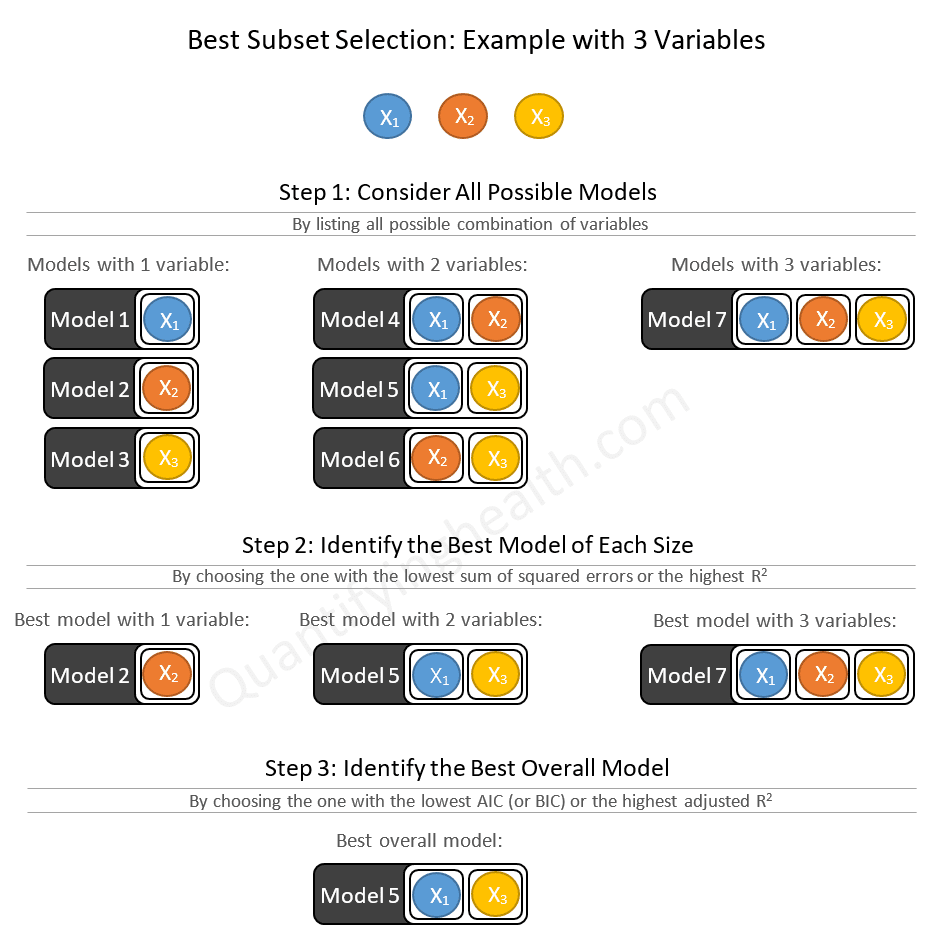
Other than enumerating all possible models (1^st step in the figure above), we have 2 key steps that we need to understand in order to develop an intuition on how the best subset algorithm is working under the hood:

How to identify the best model of each size (2^nd step in the figure above)
How to identify the best overall model (3^rd step in the figure above)

1. Determine the best model of each size

The best model can be:

The one that predicts the outcome with less errors — so the one with the lowest RSS (Residuals Sum of Squares)
Or the one that explains the largest percentage of variance of the outcome — so the one that has the largest R²

Note that in both cases the selected model will be the same.

2. Determine the best overall model

Unlike step 2, where we compared models of the same size, in step 3 we will be comparing models of different sizes, so we can no longer use RSS or R² to select the best overall model.

Why not?

Because the model with most variables is always going to have the lowest sum of squared errors and the highest R². So we cannot lose by adding more predictors, but something worse can happen which is choosing a model that overfits the data — that is closely fitting the sample data while having a low out-of-sample accuracy.

In order to deal with this problem, one solution is to choose the best overall model according to a statistic that imposes some sort of penalty on bigger models, especially when they contain additional variables that barely provide any improvement.

This is where the AIC, BIC and adjusted R² come into play.

What these will do, in simple terms, is estimate the out-of-sample accuracy.

Of course you can do better than estimating:

You can leave out part of your dataset to test these models and get a direct measure of the out-of-sample accuracy. But this can only be done in special cases where data collection is not expensive and time consuming (which is almost never the case, especially in medical research).

BOTTOM LINE:

Depending on which parameter you choose, the best overall model will be the one that has the lowest AIC, BIC, or the highest adjusted R².

Advantages and limitations of best subest selection

Advantages of best subset selection:

Best subset selection:

Improves out-of-sample accuracy (generalizability) of the regression model by eliminating unnecessary predictors
Yields a simple and easily interpretable model
Provides a reproducible and objective way to reduce the number of predictors compared to manually choosing variables which can be manipulated to serve one’s own hypotheses and interests

Note that automated variable selection is not meant to replace expert opinion. In fact, important variables judged by background knowledge should still be entered in the model even if they are statistically non-significant.

Limitations of best subset selection:

Best subset selection suffers from 2 major limitations:

1. Computational limitation:

The number of models the best subset algorithm has to consider grows exponentially with the number of predictors under consideration.

For example:

For 3 predictors, the best subset algorithm has to consider 2³ = 8 models
For 10 predictors, 2¹⁰ = 1024 models
For 20 predictors, 2²⁰ = 1,048,576 models!

2. Theoretical limitation:

The idea of considering all possible combinations of independent variables can both be seen as:

Good, because we are choosing the best model from ALL possible solutions
Bad, because choosing from thousands even millions of models can be considered p-hacking (a.k.a. data dredging), as one model can look better just by chance and end up underperforming when we try to validate it on new data

In recent years, Bertsimas et al. developed a new algorithmic approach that runs best subset selection with a sample size of 1000 and number of predictors of 100 in a matter of minutes!

According to our calculations above, for 100 predictors, the computer needs to run 1.26×10³⁰ models — which is absolutely ridiculous!

Not only did they solve the computational problem (and by the way made the algorithm available in an R package called leaps), it turned out that the problem of overfitting the sample data (the theoretical limitation) is not that limiting in practice, as the model they obtained via best subset selection outperformed LASSO and forward stepwise selection in out-of-sample prediction accuracy.

If you’re interested in this topic I suggest reading the original paper of Bertsimas et al. Best Subset Selection Via a Modern Optimization Lens and another one written as a response to the first by Hastie et al. Best Subset, Forward Stepwise, or Lasso?

References

James G, Witten D, Hastie T, Tibshirani R. An Introduction to Statistical Learning: With Applications in R. 1st ed. 2013, Corr. 7th printing 2017 edition. Springer; 2013.