An association between 2 variables X and Y cannot be interpreted as causal if it can be attributed to an alternative mechanism.
Confounding is an example of such mechanism that alters the relationship between X and Y, and therefore, leads to an over or underestimation of the true effect between them.
In its simplest form, it is due to a third variable — the confounder C — that represents a common cause:
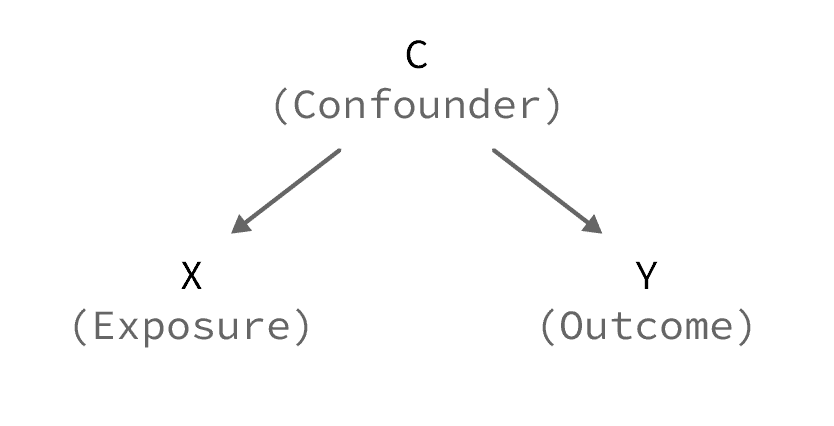
In order to uncover the true relationship between X and Y, we can use statistical techniques to control/adjust for that confounder. [If you are interested, I suggest: 7 Different Ways to Control for Confounding]
Here’s a list of 5 real-world examples where confounding explains part of, or the entire, relationship between 2 variables:
Example 1: Confounding by smoking
Description:
Alcohol consumption is associated with a higher risk of lung cancer. This association is non-causal; it is due to the confounding effect of smoking.
Visual representation:
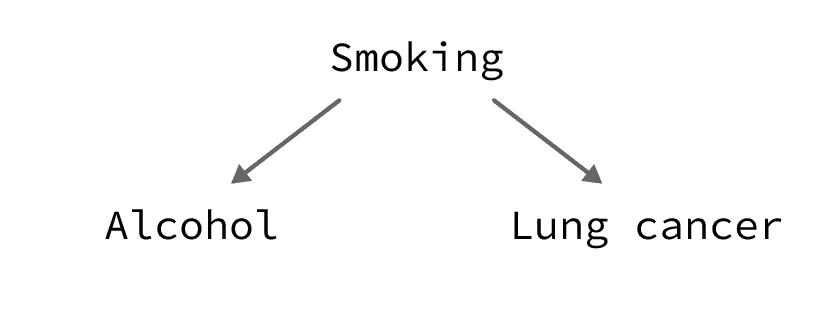
Explanation:
Alcohol consumers also tend to be smokers. And since smoking is a known cause of lung cancer, this explains the high prevalence of lung cancer in the group of alcohol consumers.
Real-world evidence:
Zang and Wynder have shown that alcohol consumption increases the odds of lung cancer by 2.4 times. However, this effect disappeared when they controlled for smoking.
Example 2: Confounding by heart disease
Description:
Low blood pressure is associated with a higher risk of mortality. This association is non-causal; it is due to the confounding effect of heart disease.
Visual representation:
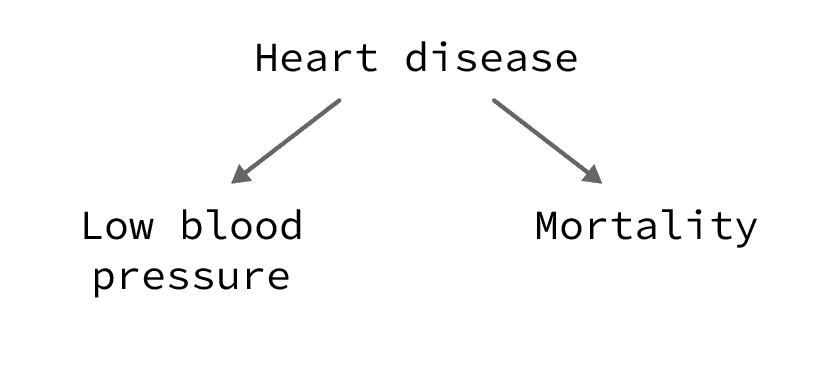
Explanation:
A low blood pressure is, in many cases, a marker of a more serious heart disease which explains the high-risk of mortality in the group of people with low blood pressure.
Real-world evidence:
Busby and colleagues demonstrated that among elderly people, those with low diastolic blood pressure have almost twice the risk of dying than those with normal blood pressure. This effect disappeared when they controlled for confounding factors such as the presence of heart disease.
Example 3: Confounding by severity
Description:
The administration route of corticosteroids for the treatment of asthma is associated with the risk of hospitalization. This association is non-causal; it is due to the confounding effect of asthma severity.
Visual representation:
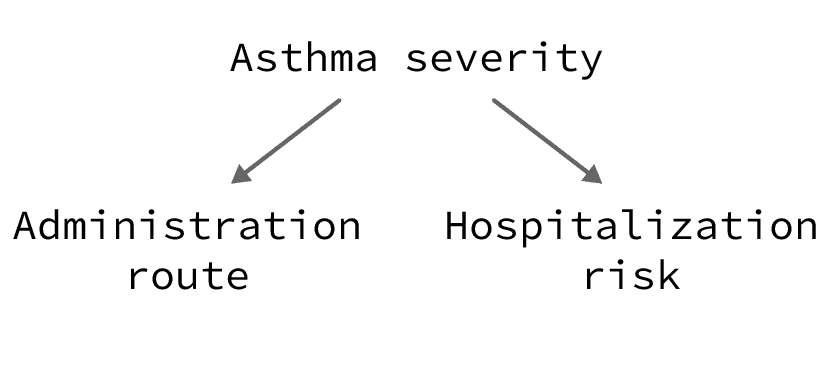
Explanation:
Severe cases of asthma require intravenous treatment with corticosteroids. These patients also have a higher risk of being hospitalized, not because they were treated intravenously, but because they have a more serious illness.
Mild cases of asthma tend to be treated orally. Also, these patients are less likely to be hospitalized.
This explains the higher risk of hospitalization in the group of intravenously treated patients.
Real-world evidence:
An observational study by Clark and colleagues reported that asthmatic patients treated with intravenous corticosteroids had 2.6 times the odds of being hospitalized compared with orally treated patients.
This effect disappeared after controlling for confounding by severity, among other factors, through the use of randomized controlled trials. In fact, a meta-analysis by Rowe and colleagues found that intravenous and oral corticosteroids are equally effective for treating asthma.
Example 4: Confounding by indication
Description:
Acetaminophen use is associated with a higher risk of mortality. This association is non-causal; it is due to the confounding effect of a serious disease such as cancer.
Visual representation:
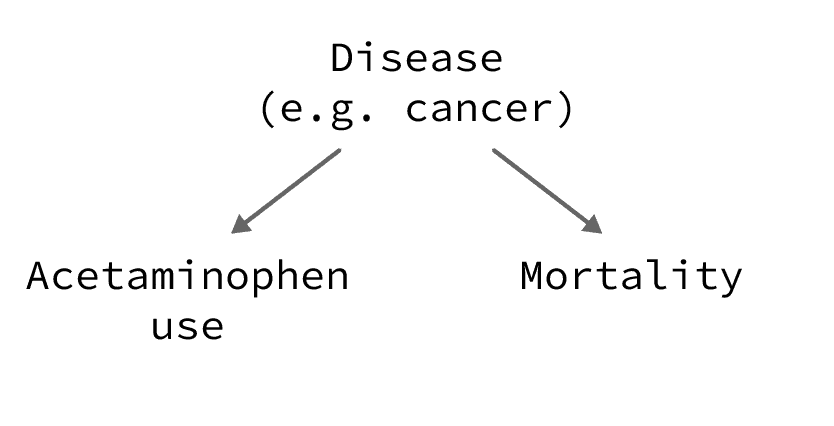
Explanation:
Serious illnesses such as cancer require analgesic treatment, of which acetaminophen. So, patients who use acetaminophen will have higher mortality rate. But this is due to their underlying illness and not to the use of acetaminophen itself.
Real-world evidence:
Lipworth and colleagues conducted a cohort study where they followed 49,890 persons who were prescribed acetaminophen. They showed that their mortality rate was nearly doubled during the first year of follow-up (i.e. during the first year after acetaminophen indication), before dropping in later years.
This just reflects the fact that analgesics, such as acetaminophen, may be prescribed for people with serious illness:
- Those who had a terminal illness died within the first year of follow-up — this explains the high mortality rate during the first year.
- Those who did not die within the first year of follow-up probably had some minor issue that required an acetaminophen prescription — this explains the drop in the mortality rate after 1 year.
In this case, to eliminate the effect of confounding by indication, we can only use the mortality rate after 1 year of acetaminophen indication. This is called applying a lag-time to the exposure (you can learn more about it in this article on protopathic bias).
Example 5: Confounding by age
Description:
In patients with heart failure, obesity is associated with a lower risk of mortality after a heart attack. This association is non-causal (i.e. does not provide evidence that obesity protects against death from heart attacks), it is due to the confounding effect of age.
Visual representation:
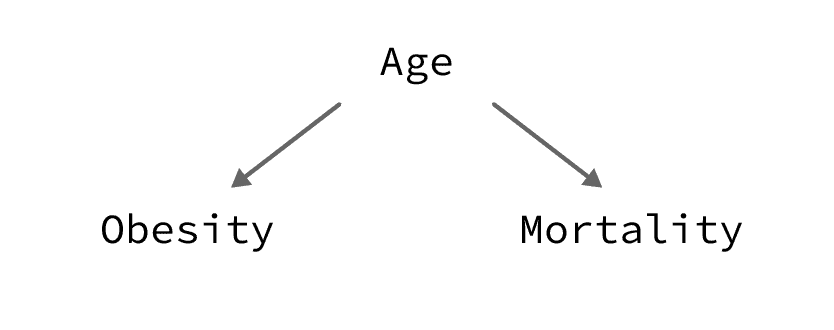
Explanation:
Heart disease is more prevalent in the elderly population. In this subgroup, obesity is less prevalent among those over 75 years (probably due to the shorter life expectancy among those with obesity [source]). As a consequence, the average obese patient with heart failure will be younger than the average non-obese patient with heart failure.
So, obese patients will have a lower mortality risk, not because of the protecting effect of obesity itself, but because of their younger age.
Real-world evidence:
Wu and colleagues found that obese patients with heart failure have 18% less risk of mortality after a heart attack. This association disappears after controlling for age.