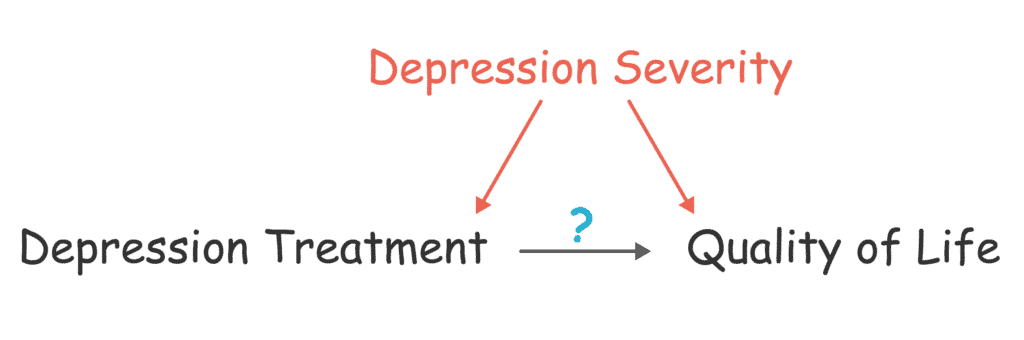
Suppose we conducted an observational study to estimate the causal effect of some depression treatment on the quality of life of patients:

The problem is that the relationship between the two is confounded by the severity of depression:

The arrows in the diagram reflect causal associations:
- The arrow from “depression severity” to “treatment” reflects the fact that people with more severe depression are more likely to be treated than those with mild depression.
- And the arrow from “depression severity” to “quality of life” reflects the fact that more severely depressed patients have a lower quality of life.
So, depression severity is a common cause of “treatment” and “quality of life” and therefore a confounder.
For more information on how to identify confounders, see: 4 Simple Ways to Identify Confounding.
Because of confounding, the treatment will be correlated with a lower quality of life — since treated individuals will mostly be those who have a more severe depression, and thus more likely to have a lower quality of life.
To measure the direct (or causal, or unconfounded) effect of treatment on the quality of life, we need to control for confounding (see: 7 Different Ways to Control for Confounding).
The simplest way is to adjust for “depression severity” by including it in the regression model used to calculate the effect of the “treatment” on the “quality of life”:
Quality of Life = β0 + β1 Treatment + β2 Depression Severity + ε
In this model, β1 will be the causal effect of “treatment” on “quality of life”.
This method is called backdoor adjustment, since we calculated the causal effect by directly adjusting for the confounder itself which lies on the backdoor path — the backdoor path is any path that relates the exposure (treatment) to the outcome (quality of life) and starts with an arrow pointing to the exposure (treatment):
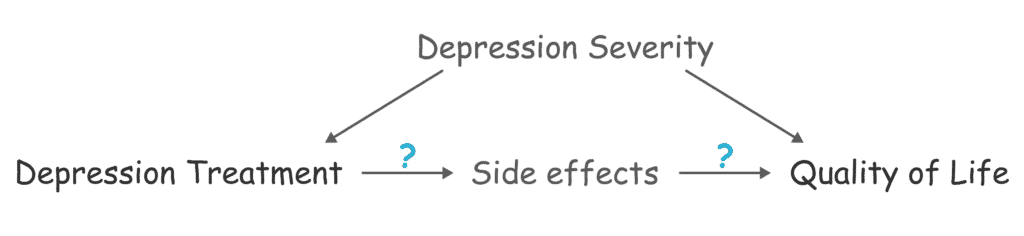
To make things harder on ourselves, suppose that depression severity was not measured in the study.
In this case, we cannot use it to control for confounding, and we should find an indirect way to calculate the causal effect of the treatment on the quality of life.
Such method exists, and it is called: front-door adjustment.
The trick is to find a mediator of the effect of “treatment” on “quality of life” that is not related to the confounder variable. For example, the “side effects” that are a consequence of the treatment and through which the treatment affects the quality of life of patients:
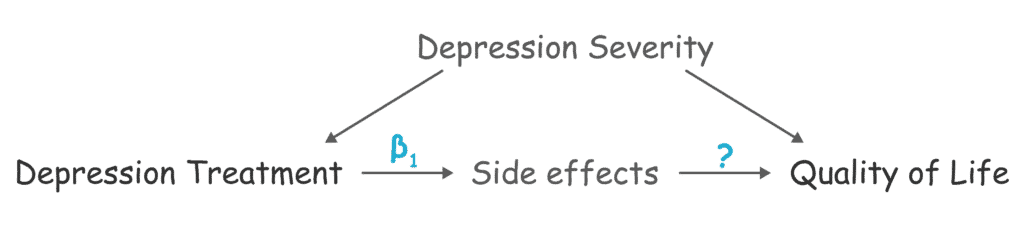
Then we measure the causal effect of the treatment on the quality of life in 2 steps:
Step #1: Calculate the causal effect of “treatment” on “side effects”
Since the relationship between “treatment” and “side effects” is unconfounded, then β1 from the following regression equation will estimate the causal effect between these 2 variables:
Side Effects = β0 + β1 Treatment + ε
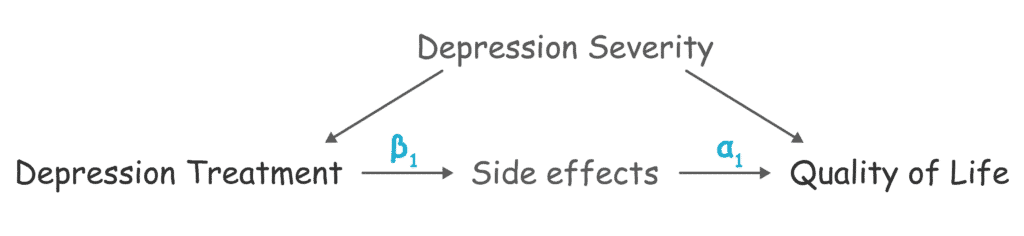
Step #2: Calculate the causal effect of “side effects” on “quality of life”
The relationship between “side effects” and “quality of life” is confounded by “depression severity” (a common cause). So, we can use backdoor adjustment and control for either “depression severity” or “treatment” to block the backdoor path.
By adjusting for treatment, the coefficient α1 from the following regression equation will estimate the causal effect of “side effects” on “quality of life”:
Quality of Life = α0 + α1 Side Effects + α2 Treatment + ε
Finally, we can multiply the 2 causal effects, the 2 coefficients, to obtain the total causal effect of the treatment on the quality of life:
The causal effect of “treatment” on “quality of life” = β1 * α1
In conclusion, the front-door adjustment allows us to control for unmeasured confounders if 2 conditions are satisfied:
- The exposure is only related to the outcome through the mediator (i.e. does not have a direct effect on the outcome).
- The mediator is not causally associated with the confounding variable.
References
- Pearl J, Mackenzie D. The Book of Why: The New Science of Cause and Effect. First edition. Basic Books; 2018.