The pretest-posttest control group design, also called the pretest-posttest randomized experimental design, is a type of experiment where participants get randomly assigned to either receive an intervention (the treatment group) or not (the control group). The outcome of interest is measured 2 times, once before the treatment group gets the intervention — the pretest — and once after it — the posttest.
The objective is to measure the effect of the intervention which can be:
- A medical treatment
- An education program
- A policy change, etc.
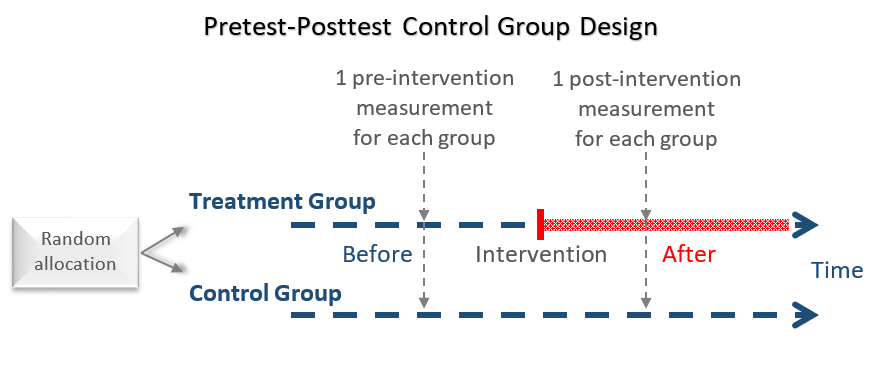
The pretest-posttest control group design has 3 major characteristics:
- The study participants are randomly assigned to either the treatment or the control group (this random assignment can occur either before of after the pretest).
- Both groups are exposed to the same conditions except for the intervention: the treatment group receives the intervention, whereas the control group does not.
- The outcome is measured simultaneously for both groups at 2 points in time — the pretest and the posttest.
The pretest-posttest control group is the most commonly used design in randomized controlled trials.
Advantages of the pretest-posttest control group design
By using a pretest, a control group, and random assignment, this design controls all internal threats to validity.
Advantage of having a pretest measurement
This design is better than the posttest-only control group design because it adds a pretest.
Adding a pretest:
- Increases the power of the design to detect an effect.
- Allows studying the effect of the intervention at different sublevels of the pretest.
- Helps analyzing initial differences between groups (and therefore quantifying their effect on the study outcome).
- Helps controlling attrition bias i.e. the unequal loss to follow-up of participants between the treatment and the control group which can affect the outcome measured at the posttest.
Advantage of using random assignment and having a control group
Random assignment and the control group will both limit the effects of:
- Selection bias: Which happens when participants themselves get to choose if they receive the intervention or not. This may create unequal and incomparable study groups. Randomization allows unbiased assignment of participants to treatment options, and therefore makes the study groups comparable.
- Maturation: Which is the effect of time (between the pretest and the posttest) on study participants (e.g. participants growing older, or getting tired over time) which might influence the outcome, thus becoming a rival explanation for the intervention regarding the study outcome. Participants are subject to maturation both in the treatment and the control group, therefore, any difference between the outcome of these groups will be due to the effect of the treatment alone and will not be affected by maturation.
- History: Which is any event that might co-occur with the intervention and has the potential to influence the outcome. Co-occurring events affect both the treatment and the control group, and therefore any difference between the outcome of these groups will be due to the effect of the treatment alone and will not be affected by history.
- Testing: Which is the effect of taking a pretest on the result of a posttest. For instance, if the pretest sensitizes participants and compels them to behave in a certain way that affects the outcome of the posttest. The presence of a control group protects against testing effects, as these will affect both groups and therefore any difference between the outcome of these groups will be due to the effect of the treatment alone and will not be affected by testing.
- Regression to the mean: When pretest scores are exceptionally good by chance, the posttest scores will naturally regress toward the mean. This happens because an exceptionally good performance is hard to maintain. Regression toward the mean can be mistaken for the effect of the treatment, and therefore is a source of bias. Since participants from both groups are subject to regression, therefore, comparing the outcome of the treatment group with that of the control group will take care of this regression effect.
Limitations of the pretest-posttest control group design
Participants included in any randomized study might not be typical people in the population i.e. they may not represent well the population of interest, this is because:
- Not everyone in the population of interest is eligible for the experiment,
- and not everyone who is eligible can be recruited,
- and not everyone who is recruited will give us their consent to be included in the study,
- and not everyone who consented will be randomized.
So the outcome of a randomized study may not generalize well to the population.
More specifically, this design:
- Does not allow us to study how the effect of the treatment changes over time: To do so, we need to add more posttest measures.
- Is susceptible for interactions between the intervention and other factors (such as the pretest, history, instrumentation, etc.): One solution for this problem is to use the Solomon four-group design.
Example of a study that used the pretest-posttest control group design
Koenig et al. used a pretest-posttest control group design to study the effect of a yoga program on the classroom behavior of autistic children. These children were randomly assigned to either receive the yoga program or their standard morning routine.
The study concluded that yoga can significantly improve the classroom behavior of autistic children.
But because the researchers used a convenience sample from a particular school and the classrooms that were allowed to participate were hand-picked by administrators, the study outcome may not generalize well to all children with autism.
References
- Campbell DT, Stanley JC. Experimental and Quasi-Experimental Designs for Research. Wadsworth; 1963.
- Reichardt CS. Quasi-Experimentation: A Guide to Design and Analysis. The Guilford Press; 2019.
- Shadish WR, Cook TD, Campbell DT. Experimental and Quasi-Experimental Designs for Generalized Causal Inference. 2nd edition. Cengage Learning; 2001.