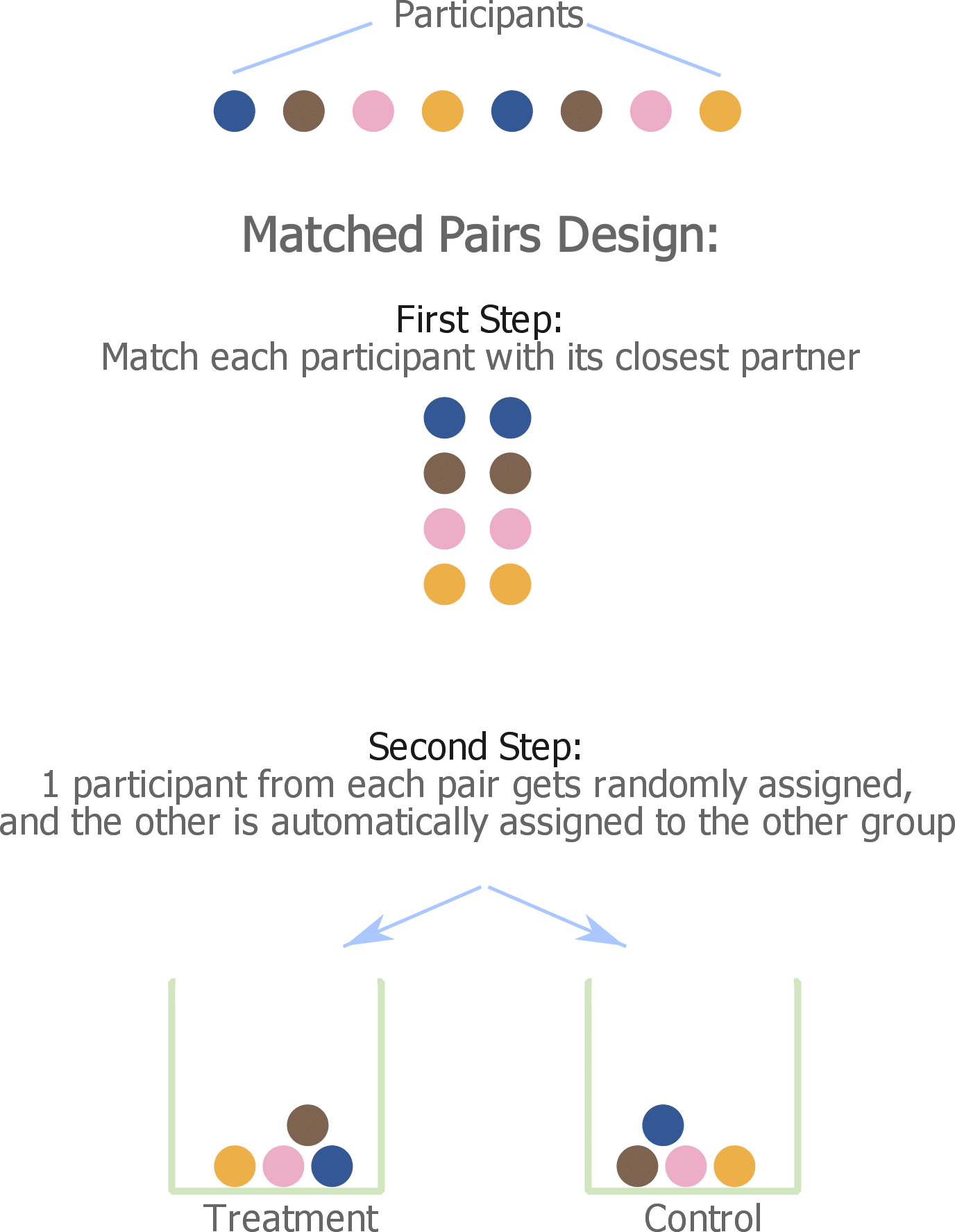
A matched pairs design is an experimental design where participants having the same characteristics get grouped into pairs, then within each pair, 1 participant gets randomly assigned to either the treatment or the control group and the other is automatically assigned to the other group.
In other words, if we take each pair alone, the choice of who gets the treatment and who doesn’t is completely randomized.
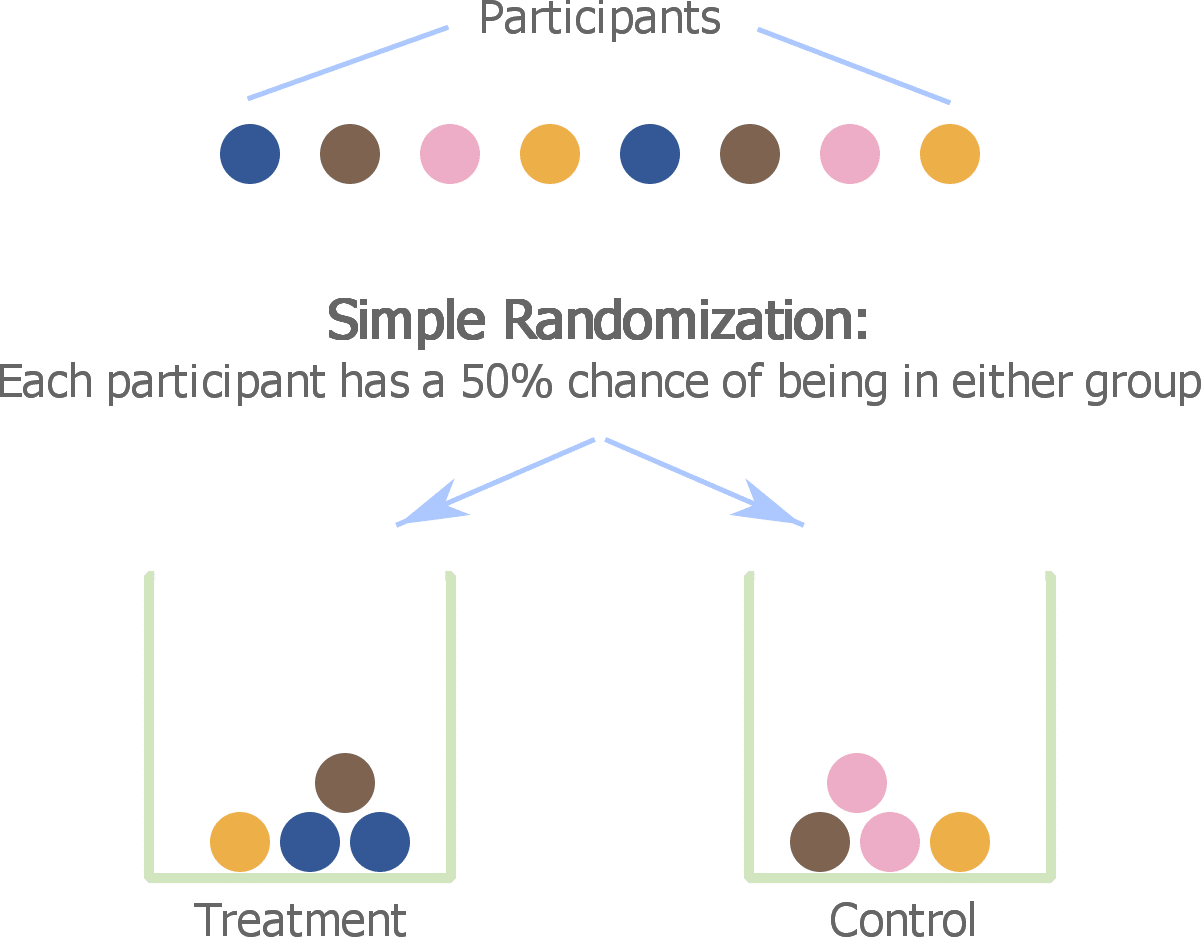
This is in contrast to a simple randomized experiment, where the list of all participants in the study gets randomized to either the treatment or the control group.
In a matched pairs design, we can choose to match on all types of variables (categorical or numerical). Here’s how it works:
- When matching on categorical variables, such as gender, the pairs should be chosen to be of the same category (both males or both females).
- When matching on a continuous variable, such as age, a range should be specified (for example a difference of no more than 10 years is tolerated between the matched pairs).
- When matching on several continuous variables, measures such as minimum Euclidean distance can be used [Source: Epidemiology Beyond the Basics]
When to use matched pairs design?
A matched pairs design is better than a simple randomized trial when we want to enforce a balance between important participant characteristics that may influence the outcome.
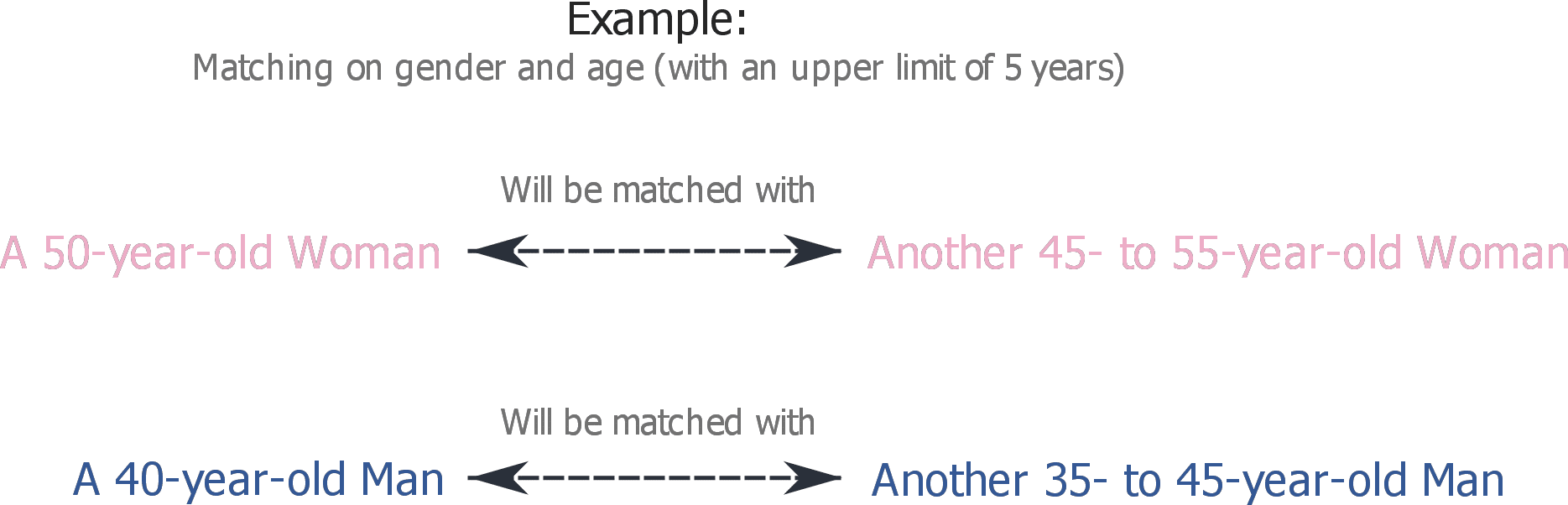
For example, a lot of outcomes are gender and age specific. Therefore, matching individuals on these 2 variables will help improve the validity of the study by reducing bias.
Here’s an example of how to match on gender and age:
Matching is particularly interesting when it involves non-modifiable predictors of the outcome.
Why?
As we will see below in the limitations of pair-matching, if a variable is used as a matching variable, its effect on the outcome can no longer be analyzed in the study.
Keep in mind that, in general, we prefer to analyze the effect of variables that CAN be modified by people, such as smoking for example. Because once we prove the influence of these risk factors on the outcome, we can takes steps to help people modify their lifestyle in a certain direction.
Variables such as gender and age cannot be modified and therefore are perfect candidates to be used for matching.
When is matching most beneficial?
Pair-matching benefits studies with small samples sizes where it is difficult to obtain balanced groups by complete random allocation.
Why not simply increase the sample size?
- Increasing the sample size generally involves higher financial costs.
- Sometimes it is practically not feasible especially when the study is limited in time and/or space.
By improving the comparability of the study participants, matching may also increase the power of the study (the probability of finding an effect when, in fact, there is one).
It also ensures the inclusion of a pre-specified number of participants from each category, therefore the results will be more generalizable.
Does a matched pairs design help control confounding?
No, since a matched pairs design is an experiment, and experimental designs are essentially not susceptible to confounding.
Note however, that matching is sometimes used in observational studies (mostly in case-control studies), and one of its main advantages there is to prevent confounding (especially when it is caused by variables that are difficult or impossible to measure).
Limitations of the matched pairs design
One of the major problems of matching is the difficulty to find appropriate matches. In some cases we may be forced to remove a number of participants from the study if appropriate matches could not be found. This may be a source of bias if participants with certain characteristics have a higher probability than others of being excluded.
Matching may be impractical in certain clinical settings where patients who arrive at the clinic must be treated immediately [Source: Fundamentals of Clinical Trials]. Sometimes it is also financially expensive to implement [Source].
In cases where matching takes a lot of time and work to implement, we can instead invest in increasing the sample size and running a simple randomized controlled experiment.
On which variable(s) should you match?
The answer to this question is not always straightforward, especially when the topic that we want to study does not have an extensive literature behind it, or worse, when the literature shows conflicting expert opinions.
This will certainly be an issue since the causal association between risk factors, matching variables and outcome should be well understood in order to decide on which variable(s) to match.
Picking the wrong matching variables is problematic as it is irreversible. In other words, we CANNOT explore alternative causal hypotheses since the design is definitive and cannot be changed.
On how many variables should you match?
A certain trade-off exists when choosing the number of matching variables:
- Matching on 1 variable will not be enough in some cases because the pairs will not be close enough
- Matching on too many variables will lead to overmatching because the selected pairs become too similar
As the number of variables that we are matching on increases, so does the probability of these being associated with the risk factor which effect we wish to analyze. This may reduce the statistical power of the study.
Imagine for example matching individuals on age, gender, BMI and socio-economic factors, this would certainly compromise the ability to study the effect of cholesterol levels on heart disease, since all these matching variables are somewhat related to cholesterol levels.
Another problem of matching on several variables is that it increases the difficulty of finding appropriate matches.
Matching also eliminates the possibility of studying the effect of matching variables on the outcome (for example as a secondary objective of the study).
Finally, for large sample sizes, matching is not necessary since the study groups are already balanced at baseline just by randomn assignment.
How to deal with these limitations?
Here are 2 examples where matching is easy, cheap and makes perfect sense to implement:
- The first interesting special case is when we can use the same participant both in the treatment and control groups (a classical example would be to use the right and left arm/eye/ear to experiment with a new medical treatment). In this case, each participant would be his/her own pair.
- The other example is matching twins to control for genetic and environmental/familial factors, which is a lot easier and cheaper than measuring these genetic and environmental factors and adjusting for them when analyzing the study data.
References
- White H, Sabarwal S, de Hoop T. Randomized Controlled Trials (RCTs). Randomized Control Trials.:15.
- Balzer LB, Petersen ML, van der Laan MJ. Adaptive pair-matching in randomized trials with unbiased and efficient effect estimation. Stat Med. 2015;34(6):999-1011. doi:10.1002/sim.6380
- Klar N, Donner A. The merits of matching in community intervention trials: a cautionary tale. Stat Med. 1997;16(15):1753-1764. doi:10.1002/(sici)1097-0258(19970815)16:15<1753::aid-sim597>3.0.co;2-e
- Bai Y. Optimality of Matched-Pair Designs in Randomized Controlled Trials. SSRN Electron J. Published online 2019. doi:10.2139/ssrn.3483834
- Hulley S, Newman T. Designing Clinical Research. Fourth edition. LWW; 2013.