Short answer:
Correlation implies causation when alternative explanations of the relationship between the correlated variables (such as confounding and bias) are removed (by appropriately modifying the study design) or controlled for (by adjusting for them in the statistical analysis).
Explanation:
Causation means that changing the treatment X for a person will affect the probability of the outcome Y for that person. Correlation means that people with different values of X tend to have different values of Y (so changing X does not necessarily affect Y).
In Statistics 101, every student learns to chant, “Correlation is not causation.” With good reason!
The book of Why, Judea Pearl.
The problem is that everyone is interested in causation, but instead most studies report correlation (or association), for example: “Strawberry is correlated with a lower risk of cancer”.
So, what does the strawberry-cancer correlation mean in practice?
Should you start eating more strawberries? Should doctors recommend strawberries to high-risk patients to reduce their risk of cancer?
The answer to both questions is no. But why not?
Because this correlation can be explained in a million ways without assuming a direct (causal) effect of strawberries on cancer.
For instance, people who are health-conscious have a higher probability than average of: eating more fruits (such as strawberries), being non-smokers, and exercising more, therefore explaining the correlation between strawberry and the lower risk of cancer by the overall healthier lifestyle and not strawberry consumption in particular.
Which types of studies are allowed to talk about causation?
The previous paragraph teaches us that if we want to compare 2 groups of people, e.g. those who eat strawberry and those who don’t, we should be certain that they are similar in every possible way except for eating strawberry. If we found such groups, then any correlation between strawberry and cancer can now be considered as evidence of a causal relationship.
Randomized controlled trials have long been the only type of study that can address causal questions since they equalize groups by randomly assigning people into:
- Those who are given the treatment (the treatment group), and
- Those who are not (the control group).
By using randomness to divide people, we ensure that the 2 groups are similar in every possible way except for the treatment. So, any correlation between the treatment and the outcome can now be interpreted as a causal association.
For this reason, randomized controlled trials have been considered the “gold standard” of epidemiologic studies.
Observational studies, on the other hand, where participants themselves choose whether or not to take the treatment (and the researcher is just an observer of the events), have been advised to report only correlation (and not causation) between treatment and outcome.
This is because of the baseline differences between the treatment and the control groups that represent alternative (non-causal) explanations of the relationship between the treatment and the outcome.
In theory, if we can account for all these alternative explanations — by appropriately modifying the study design or adjusting for them in the statistical analysis of the data — then there would be no problem for an observational study to answer a causal question.
In fact, the whole field of causal inference is concerned with proving causal relationships from observational data. After all, how do you think researchers proved that smoking caused cancer? Certainly you did not presume that they randomized people to smoking!
An important question remains:
What exactly are these alternative explanations?
Alternative explanations are the result of 2 things: confounding and bias.
1. Confounding
Confounding is a real but non-causal association between 2 variables. This happens when the variables of interest (the treatment and the outcome) share a common cause.
For example, smoking increases the probability of both alcohol consumption and lung cancer:
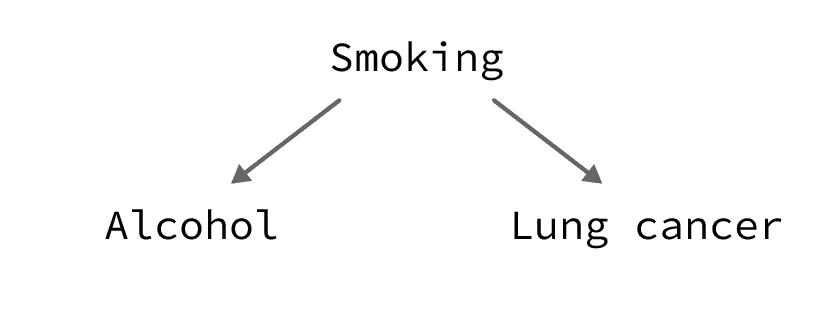
So, alcohol consumption is expected to be correlated with lung cancer, even if the 2 are not causally related.
2. Bias
Bias is an error in the estimation of an association between an exposure and an outcome due to a flaw in the design or conduct of the study.
An example would be temporal bias which happens when the treatment (or exposure) and the outcome are measured at the same time (e.g. in a cross-sectional study) which makes it hard to determine which came first. So, a correlation between X and Y could be explained by X causing Y or Y causing X.
There are many other types of biases. If you are interested, here’s a list of all biases in research.
How can we be sure that we enumerated all possible alternative explanations?
There is no way to determine if we accounted for all possible bias and confounding in a study.
The more theoretical knowledge we have on the subject (i.e. the more alternative explanations we can think of), the better we are at controlling bias and confounding.
This is why researchers should be careful with interpreting the results of observational studies, especially the ones that are exploring new fields or relationships that we do not have enough background knowledge about.
Research is all about accumulating evidence on a certain topic: the more studies we conduct, the more we build evidence for or against our hypotheses. While new stuff is interesting to work on, such studies have a higher risk of being wrong (see: Why Most Published Research Findings are False, John Ioannidis).
Too bad, but this is how it is.
If you don’t like it, go somewhere else!
Richard Feynman
That somewhere else can be the field of predictive modeling. For example, your research question could be whether we can predict the probability of lung cancer given that a person drinks alcohol.
This is a very legitimate question, and it is not related to causality.
In this case, correlation would be enough to flag alcohol consumers as a high-risk group even though alcohol itself does not (or might not) cause lung cancer, nonetheless you would have shown that alcohol consumers have a higher risk of developing lung cancer than average.