Length time bias occurs when cases who were detected earlier by SCREENING seem to have survived longer than cases DIAGNOSED after symptoms appear just because screening tests tend to identify less aggressive cases of the disease more often than aggressive ones.
When screening a population, we can imagine that the slower-developing cases of a disease will have a higher probability of being detected by the screening test than the more aggressive cases, simply because of their larger time window (see the figure below).
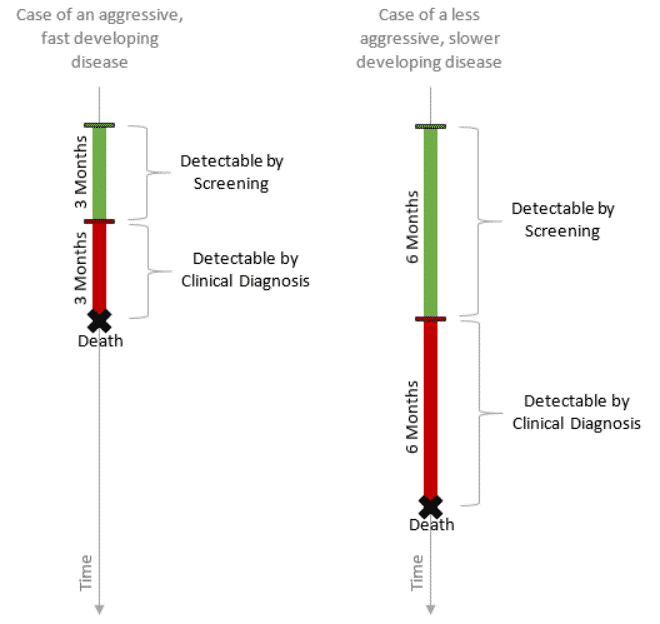
Therefore, in general, screened patients will probably have a less-aggressive version of the disease than those diagnosed according to clinical symptoms.
This can happen when we have a disease that presents a varying degree of aggressiveness between patients.
A good example is HIV:
According to health.vic.gov.au, the interval from HIV infection to the appearance of clinical signs ranges from 9 months to 20 years, with some people never reaching the clinical phase.
Notice the large variance in the incubation period: [9 months – 20 years] !!
Now suppose we want to determine if screening for HIV is helpful or not for these patients. So we conducted a study where we compared the survival between a group of screened HIV patients with a group of non-screened HIV patients (i.e. diagnosed after appearance of clinical symptoms).
Our study will be susceptible to length time bias because patients in the screened group will live longer than those in the unscreened group, but not because screening saved their lives, but because the screened group includes more of the less-aggressive cases, and those tend to live longer on average.
How to avoid length time bias
We can correct for length time bias by running a randomized controlled trial where one group gets screening and the other one is a control.
Then the trick is to compare the outcome(s) of interest between the 2 randomized groups, and NOT those who received screening versus those diagnosed after the symptoms appeared. This way we won’t be subject to length time bias.
But why?
Consider the following example:
Suppose we conducted a randomized controlled trial and divided the participants at random into 2 groups:
- A group that will receive screening
- The control group
Then we compare the mean survival time in group 1 with the mean in group 2. If group 1 survived longer than group 2, than we can conclude that screening reduced mortality.
Why aren’t we subject to length time bias here?
Because randomization equalizes the groups in terms of aggressiveness of the disease.