In this tutorial, we will use a linear regression model to examine the relationship between the Google search trends for the terms headache and ibuprofen.
1. Prepare the data
1.1. Download the data
The package gtrendsR presents an interface to retrieve the number of Google searches over time for a specific term:
library(gtrendsR)
# download trends for the words "headache" and "ibuprofen"
raw_data <- gtrends(c("headache", "ibuprofen"),
time = "2020-01-01 2023-01-01",
gprop = "web",
onlyInterest = TRUE)$interest_over_time
head(raw_data)
# date hits keyword geo time gprop category
#1 2020-01-05 43 headache world 2020-01-01 2023-01-01 web 0
#2 2020-01-12 41 headache world 2020-01-01 2023-01-01 web 0
#3 2020-01-19 42 headache world 2020-01-01 2023-01-01 web 0
#4 2020-01-26 41 headache world 2020-01-01 2023-01-01 web 0
#5 2020-02-02 40 headache world 2020-01-01 2023-01-01 web 0
#6 2020-02-09 41 headache world 2020-01-01 2023-01-01 web 0
1.2. Plot the trends
library(fpp3) # to work with time series data raw_data |> ggplot(aes(x = date, y = hits, color = keyword)) + geom_line()
Output:
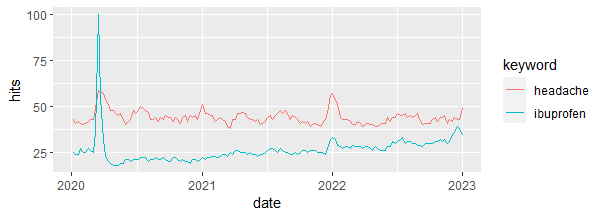
1.3. Group data by month
trends_df <-
as_tibble(raw_data) |>
group_by(year = year(date),
month = month(date),
keyword) |>
count(wt = hits, name = "hits")
trends_df
## A tibble: 74 × 4
## Groups: year, month, keyword [74]
# year month keyword hits
# <dbl> <dbl> <chr> <int>
# 1 2020 1 headache 167
# 2 2020 1 ibuprofen 100
# 3 2020 2 headache 166
# 4 2020 2 ibuprofen 103
# 5 2020 3 headache 266
# 6 2020 3 ibuprofen 248
# 7 2020 4 headache 201
# 8 2020 4 ibuprofen 80
# 9 2020 5 headache 220
#10 2020 5 ibuprofen 95
## ℹ 64 more rows
## ℹ Use `print(n = ...)` to see more rows
Next, we will create 2 separate variables (headache and ibuprofen) from the column keyword:
trends_df <- trends_df |>
pivot_wider(names_from = keyword,
values_from = hits)
trends_df
## A tibble: 37 × 4
## Groups: year, month [37]
# year month headache ibuprofen
# <dbl> <dbl> <int> <int>
# 1 2020 1 167 100
# 2 2020 2 166 103
# 3 2020 3 266 248
# 4 2020 4 201 80
# 5 2020 5 220 95
# 6 2020 6 179 83
# 7 2020 7 195 87
# 8 2020 8 219 105
# 9 2020 9 176 84
#10 2020 10 173 85
## ℹ 27 more rows
## ℹ Use `print(n = ...)` to see more rows
And we plot the relationship between headache and ibuprofen:
trends_df |> ggplot(aes(x = ibuprofen, y = headache)) + geom_point() + geom_smooth(method = "lm", se = FALSE)
Output:
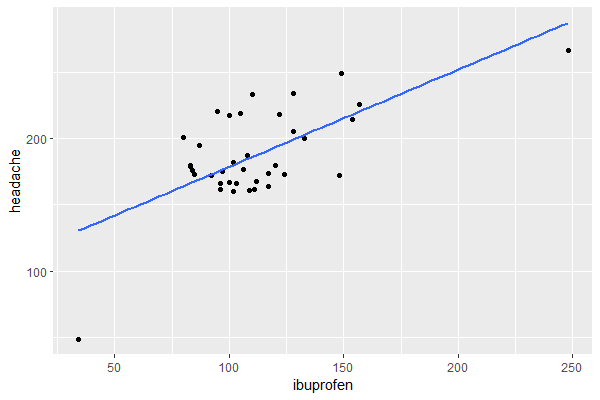
The relationship looks somewhat linear, so a linear regression model will be appropriate.
As a last step in the data transformation, we group the month and year variables into 1 variable and we transform the data frame into a time series table (tsibble):
trends_ts <- trends_df |> unite(date, year, month) |> mutate(date = yearmonth(date)) |> as_tsibble(index = date) trends_ts ## A tsibble: 37 x 3 [1M] # date headache ibuprofen # <mth> <int> <int> # 1 2020 Jan 167 100 # 2 2020 Feb 166 103 # 3 2020 Mar 266 248 # 4 2020 Apr 201 80 # 5 2020 May 220 95 # 6 2020 Jun 179 83 # 7 2020 Jul 195 87 # 8 2020 Aug 219 105 # 9 2020 Sep 176 84 #10 2020 Oct 173 85 ## ℹ 27 more rows ## ℹ Use `print(n = ...)` to see more rows
2. Run linear regression
2.1. Run linear regression and check the output
We will now use a Time Series Linear Model (TSLM) to investigate the degree of association between the Google search frequencies of the words headache and ibuprofen.
lin_reg <- model(trends_ts, TSLM(headache ~ ibuprofen)) report(lin_reg) #Series: headache #Model: TSLM # #Residuals: # Min 1Q Median 3Q Max #-81.409 -17.114 -1.486 13.753 47.006 # #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 105.5416 15.9110 6.633 1.14e-07 *** #ibuprofen 0.7314 0.1370 5.339 5.74e-06 *** #--- #Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # #Residual standard error: 27.15 on 35 degrees of freedom #Multiple R-squared: 0.4489, Adjusted R-squared: 0.4331 #F-statistic: 28.51 on 1 and 35 DF, p-value: 5.7435e-06
The model shows that the relationship is positive and statistically significant.
But maybe we can do better by adding a linear trend as a predictor in the model (this is equivalent to adding a variable that represents row numbers):
lin_reg <- model(trends_ts, TSLM(headache ~ ibuprofen + trend())) report(lin_reg) #Series: headache #Model: TSLM # #Residuals: # Min 1Q Median 3Q Max #-52.175 -10.126 -1.794 13.898 40.361 # #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 124.6388 14.2737 8.732 3.33e-10 *** #ibuprofen 0.7972 0.1167 6.832 7.30e-08 *** #trend() -1.3914 0.3561 -3.907 0.000422 *** #--- #Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # #Residual standard error: 22.89 on 34 degrees of freedom #Multiple R-squared: 0.6197, Adjusted R-squared: 0.5973 #F-statistic: 27.7 on 2 and 34 DF, p-value: 7.2947e-08
Indeed, the model is now better as the trend variable is statistically significant and the adjusted R-squared is higher than the previous model.
2.2. Check how well the fitted values match the actual values
We will do this by comparing the plot of the time series for the fitted values and the actual trend of headache:
fitted <- augment(lin_reg) fitted ## A tsibble: 37 x 6 [1M] ## Key: .model [1] # .model date headache .fitted .resid .innov # <chr> <mth> <int> <dbl> <dbl> <dbl> # 1 TSLM(headache ~ ibuprofen + trend()) 2020 Jan 167 203. -36.0 -36.0 # 2 TSLM(headache ~ ibuprofen + trend()) 2020 Feb 166 204. -38.0 -38.0 # 3 TSLM(headache ~ ibuprofen + trend()) 2020 Mar 266 318. -52.2 -52.2 # 4 TSLM(headache ~ ibuprofen + trend()) 2020 Apr 201 183. 18.1 18.1 # 5 TSLM(headache ~ ibuprofen + trend()) 2020 May 220 193. 26.6 26.6 # 6 TSLM(headache ~ ibuprofen + trend()) 2020 Jun 179 182. -3.46 -3.46 # 7 TSLM(headache ~ ibuprofen + trend()) 2020 Jul 195 184. 10.7 10.7 # 8 TSLM(headache ~ ibuprofen + trend()) 2020 Aug 219 197. 21.8 21.8 # 9 TSLM(headache ~ ibuprofen + trend()) 2020 Sep 176 179. -3.08 -3.08 #10 TSLM(headache ~ ibuprofen + trend()) 2020 Oct 173 178. -5.49 -5.49 ## ℹ 27 more rows ## ℹ Use `print(n = ...)` to see more rows fitted |> ggplot(aes(x = date)) + geom_line(aes(y = headache)) + geom_line(aes(y = .fitted), color = "red")
Output:
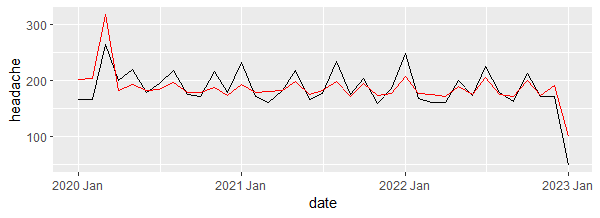
The plot shows that the model produced values that are close enough to the real values.
3. Check linear regression assumptions
Assumptions #1 and #2: the residuals must be uncorrelated and normally distributed
gg_tsresiduals(lin_reg)
Output:
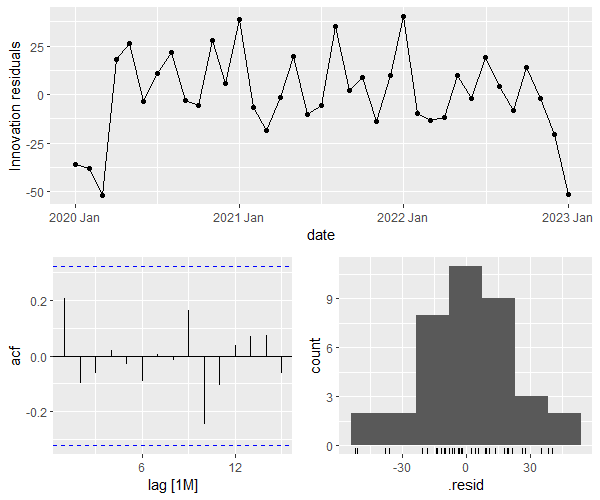
The bottom left plot shows that the residuals are not autocorrelated (since no spike surpasses the blue borders), and the bottom right plot shows that the residuals’ distribution is close to normal.
We can also check the Ljung-Box test, where:
- H0: the residuals are independently distributed (not autocorrelated).
- H1: the residuals are autocorrelated.
# we use lag = 10 as recommended by Hyndman and Athanasopoulos (see references below) features(fitted, .resid, ljung_box, lag = 10) ## A tibble: 1 × 3 # .model lb_stat lb_pvalue # <chr> <dbl> <dbl> #1 TSLM(headache ~ ibuprofen + trend()) 7.31 0.696
The test is not statistically significant meaning that we don’t have enough evidence that the residuals are autocorrelated (which is what we want).
Assumption #3: the residuals must have equal variance (i.e. homoscedastic)
augment(lin_reg) |> ggplot(aes(x = .fitted, y = .resid)) + geom_point()
Output:
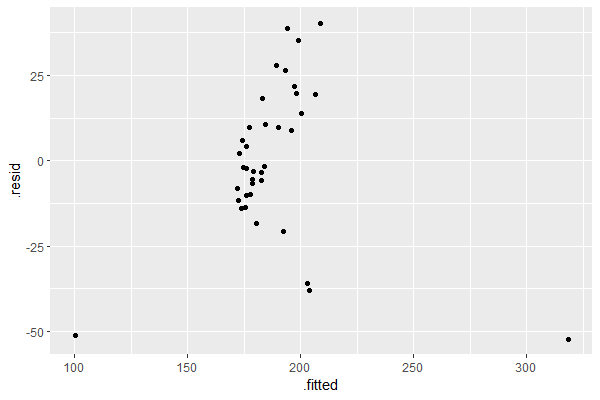
This assumption is satisfied since the plot of the residuals versus the fitted values does not show any discernible pattern, i.e. no fan, blob, or butterfly shape (for more information see: Understand Linear Regression Assumptions).
Assumption #4: the residuals must not be related to the predictor(s)
If the plot of the residuals versus any of the predictors in the linear model shows a discernible pattern, this means that the relationship may be non-linear and should be accounted for in the model.
resid_df <- residuals(lin_reg) |> left_join(trends_ts, join_by(date)) resid_df ## A tsibble: 37 x 5 [1M] ## Key: .model [1] # .model date .resid headache ibuprofen # <chr> <mth> <dbl> <int> <int> # 1 TSLM(headache ~ ibuprofen + trend()) 2020 Jan -36.0 167 100 # 2 TSLM(headache ~ ibuprofen + trend()) 2020 Feb -38.0 166 103 # 3 TSLM(headache ~ ibuprofen + trend()) 2020 Mar -52.2 266 248 # 4 TSLM(headache ~ ibuprofen + trend()) 2020 Apr 18.1 201 80 # 5 TSLM(headache ~ ibuprofen + trend()) 2020 May 26.6 220 95 # 6 TSLM(headache ~ ibuprofen + trend()) 2020 Jun -3.46 179 83 # 7 TSLM(headache ~ ibuprofen + trend()) 2020 Jul 10.7 195 87 # 8 TSLM(headache ~ ibuprofen + trend()) 2020 Aug 21.8 219 105 # 9 TSLM(headache ~ ibuprofen + trend()) 2020 Sep -3.08 176 84 #10 TSLM(headache ~ ibuprofen + trend()) 2020 Oct -5.49 173 85 ## ℹ 27 more rows ## ℹ Use `print(n = ...)` to see more rows resid_df |> ggplot(aes(x = ibuprofen, y = .resid)) + geom_point()
Output:
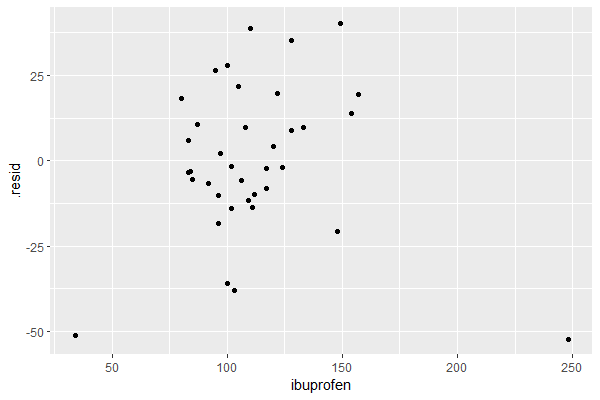
The plot shows no discernible pattern, suggesting that the linear model is a good fit to the data.
References
- Hyndman RJ, Athanasopoulos G. Forecasting: Principles and Practice. 3rd ed. edition. Otexts; 2021.