Which Variables Should You Include in a Regression Model?

When building a linear or logistic regression model, you should consider including:

Variables that are already proven in the literature to be related to the outcome
Variables that can either be considered the cause of the exposure, the outcome, or both
Interaction terms of variables that have large main effects

However, you should watch out for:

Variables that have a large number of missing values or low variability
Variables that are highly correlated with other predictors in the model (causing a collinearity problem)
Variables that are not linearly related to the outcome (in case you’re running a linear regression)

Below we discuss each of these points in details.

1. Selecting variables based on background knowledge

Advantages of using background knowledge to select variables

It provides a way to incorporate and combine previous information from a variety of high quality studies.
Selection happens before running any analysis (i.e. before uncovering what your data have to say), therefore, not prone to overfitting your sample data.

How to choose variables based on background knowledge?

You can find out whether a given variable is already proven to be related to the outcome of interest by:

reviewing previous literature on the subject
consulting experts in the field

Note:
Q: Why should you limit your work to boundaries set by previous studies? After all isn’t the purpose of research to discover new causes and relationships?
A: The probability that a finding is true given a statistically significant result (also called Positive Predictive Value) depends a lot on its pre-study odds [Ioannidis, 2005]. Therefore, research findings are more likely to be true after confirmation from MANY studies.
So:

Confirming and replicating other study results is AS IMPORTANT AS exploring data to discover new relationships.

2. Selecting variables based on causal relationships

Advantages of selecting variables based on causality

Regression models are built for 2 reasons:

either to explain the relationship between an exposure and an outcome — We will refer to these as explanatory models
or to predict the outcome based on a set of independent variables — We will refer to these as prediction models

Whether you’re building an explanatory model or a prediction model, understanding the causal structure of the problem is useful:

in explanatory models, it helps you avoid confounding and selection bias
in prediction models, it helps you:
1. get rid of unnecessary variables
2. substitute some variables with others that will yield similar prediction accuracy while being cheaper/easier to collect

How to choose variables based on causal understanding?

Good news! You don’t need to determine the causal relationship between ALL variables in your model. In practice, you can make use of a simple rule, the disjunctive cause criterion, which states that:

You should control for variables that either cause the exposure, or the outcome, or both.
VanderWeele et al., 2011

If you are interested in selecting variables based on causal assumptions, I highly recommend my other article: Using the 4 D-Separation Rules to Study a Causal Association.

3. Including interaction terms

Interaction occurs when one variable X₁ affects the outcome Y differently depending on the value of another variable X₂.

A good example of an interaction is between genome and environment as causes of disease.

Having one of them increases the risk of getting the disease, but together they will have a synergistic effect that will increase the risk substantially.

In order to account for this interaction, the equation of linear regression should be changed from:

Y = β₀ + β₁X₁ + β₂X₂ + ε

to:

Y = β₀ + β₁X₁ + β₂X₂ + β₃X₁X₂ + ε

⚠ Note:
You should decide which interaction terms you want to include in the model BEFORE running the model. Trying different interactions and keeping the ones that have a significant coefficient is a form of data dredging (also called p-value hacking) and therefore is not recommended.

In practice, include:

interactions that were proved to be important in previous studies.
interaction terms for variables that have large main effects as these will probably have significant coefficients.

For more information, I have a separate article on Why and When to Include Interactions in a Regression Model.

4. Handling missing values and low variability

4.1. Missing values

Handling missing data is not always a straightforward matter.

For instance, it is NOT recommended to exclude a variable based ONLY on some percentage of missing values.

Other factors should be taken into consideration, such as:

Why are these values missing? Are they missing at random? For example, if more extreme values were more likely to be missing, exclusion of the variable from the model may be a better solution than imputation.
How much is this variable important in your analysis? The more important the variable, the less percentage of missing values we can tolerate.
Given that some percentage of values is missing, can this variable still carry some information to explain the outcome?

While most references suggest removing a variable that has most of its values missing, it is less clear what to do in intermediate cases.

To make things easier for practitioners, I wrote a quick guide for beginners on how to handle missing data.

4.2. Low variability

In general, independent variables need some variability in order to be good predictors in a model.

For instance, an underrepresented category in a variable (for example 195 non-smokers versus 5 smokers) is, in most cases, a good reason to remove the variable from the model. Although sometimes these variables can still be useful, for instance, when the outcome is lung cancer, even a highly skewed smoking variable may still be a good predictor.

BOTTOM LINE:

Variability should be considered together with the importance of the variable to decide whether to exclude it or not from the model.

5. Avoiding collinearity when selecting predictors

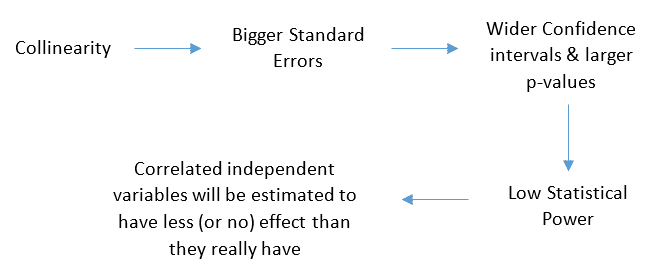
When 2 or more independent variables in a model are highly correlated we say that we have a collinearity problem.

Collinearity is not a binary issue: either we have it or we don’t. Instead, the stronger the correlation between inputs of the regression model, the more serious the problem is.

When variables are highly correlated, it becomes hard to correctly estimate the contribution of each single one of them.

Here’s how collinearity may affect the model:

How to detect collinearity?

Not all collinearity problems can be detected by inspection of the correlation matrix. This is because a correlation matrix shows correlation between PAIRS of variables.

Sometimes collinearity exists between 3 or more variables — multicollinearity, and this can be detected by looking at the VIF (Variance Inflation Factor).

In general, a VIF > 10 indicates a multicollinearity issue. Although, this is not carved in stone because sometimes multicollinearity can be present even with a VIF < 5 [Vatcheva et al., 2016].

BOTTOM LINE:

Once collinearity is detected, the simplest solution is to keep the most important of the variables that are causing the problem and drop the rest.

6. Including variables that are not linearly related to the outcome

This part only applies to linear regression, where we assume that the relationship between predictors and outcome should be a straight line.

Don’t underestimate the importance of this assumption, because when violated, all of the linear model’s output is USELESS.

Instead of plotting each independent variable versus the outcome, we can instead plot residuals of the regression model versus fitted values. The plot should show a linear pattern, otherwise, consider using a log transformation or a non-linear model to fit your data.

(For more information, see: Understand Linear Regression Assumptions)

What if you ended up with a large number of predictors?

When fitting a linear regression model, the number of observations should be at least 15 times larger than the number of predictors in the model. For a logistic regression, the count of the smallest group in the outcome variable should be at least 15 times the number of predictors. Otherwise, the model will not be generalizable — its out of sample accuracy will be low because of overfitting.

You can reduce the number of candidate predictors by:

Grouping similar variables: Either by using domain knowledge, for example replacing all diseases that affect heart muscles, valves, rhythm and blood vessels with one variable — cardiovascular disease. Or based on statistical methods like PCA (Principle Components Analysis) which summarizes the large initial set of variables by replacing them with 2 or 3 principle components that maintain the largest possible variability in the data. Grouping variables has the downside of getting a coefficient for the combined variables only, therefore losing the details on the effect of each.
Running a LASSO regression: LASSO is a regularized regression model that shrinks the coefficients of unimportant predictors to zero, thus performing automatic variable selection. However, all coefficients will be shrunk and the effect of each predictor will appear lower than it really is.
Using stepwise variable selection: Despite its popularity, stepwise regression has a lot of limitations that you should be aware of before using it. Check out Understand Forward and Backward Stepwise Regression.
Using univariate variable selection: Another popular and highly criticized method is to run a hypothesis test on each candidate variable, then in the final model only include those that had a p-value < 0.2 for example. This approach is just a variant of stepwise selection and therefore inherits the same problems of the stepwise method [Source: Clinical prediction models, 2nd edition].
Selecting variables that have the largest variance: In cases where you have thousands of predictors, it is common to reduce their number by only selecting those with the highest overall variability as these are more likely to be predictive of the outcome. The advantage of using such method to select predictors regardless to the outcome variable is that it does not bias the regression results.

As a rule of thumb:

When selecting independent variables for a regression model, avoid using multiple testing methods and rely more on common sense and your background knowledge.